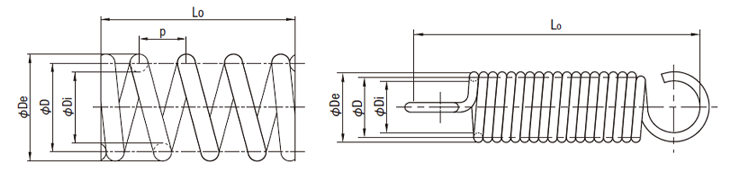
Spring Calculations (Excerpt from JIS B 2701-1:2018)

• Symbols Used in Spring Design Equations
• Basic Formula Used in Spring Design
• Matters for Consideration in Spring Design

Symbols Used in Spring Design Equations

Symbol meaning

Symbol	Symbol meaning	Unit
c	Spring index c = D/d	ー
D	Average coil diameter D = (Di + De)/2	mm
De	Coil outer diameter	mm
Di	Coil inner diameter	mm
d	Wire diameter (wire diameter to be used in calculation or diameter of product material)	mm
F	Spring force or force acting on spring (load)	N
Fi	Initial tension of tension spring	N
fe	Natural frequency	Hz
G	Modulus of transverse elasticity	N/mm2
Lc	Closed length of compression spring	mm
Lo	Custom length of compression spring or custom length of tension spring	mm
ms	Weight of spring moving parts	kg
n	Effective number of coils of compression spring or number of coils of tension spring	ー
nt	Total number of coils	ー
p	Spring pitch	mm
R	Spring constant of compression spring and tension spring	N/mm
s	Deflection of compression spring and tension spring	mm
U	Energy stored in spring	J
κ	Shear stress correction factor	ー
ρ	Weight per unit volume of material (density)	kg/mm3
σB	Tensile strength of material	N/mm2
Τκ	Shear correction stress	N/mm2
Τo,i	Initial shear non-correction stress of tension spring	N/mm2
Τo	Shear non-correction stress of compression spring or tension spring	N/mm2

Basic Formula Used in Spring Design

When designing compression springs

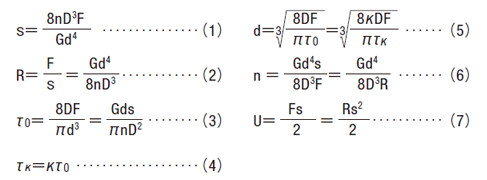
When designing tension springs with initial tension When there is no initial tension Fi = to, i = 0

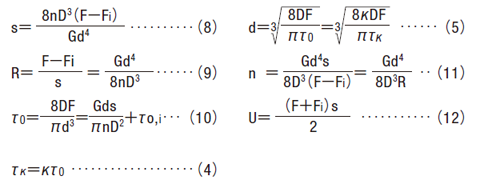
Matters for Consideration in Spring Design

Modulus of transverse elasticity (main materials)

Unit: N/mm²

Material		G value
Spring steel material Hard steel wire Piano wire Oil tempered wire		7.85x104
Stainless steel wire for springs	SUS302 SUS304 SUS304n1 SUS316	6.85x104
	SUS631J1	7.35x104
Brass wire Nickel silver wire		3.90x104
Phosphor bronze wire		4.20x104
Beryllium copper wire		4.40x104

Effective number of coils

The effective number of coils used in spring design depends on the following.
Characteristics can become unstable when using less than three effective coils, and so more than three should be used.

For compression springs

For compression springs, the effective number of coils depends on the following.
n=nt-(X1+X2)
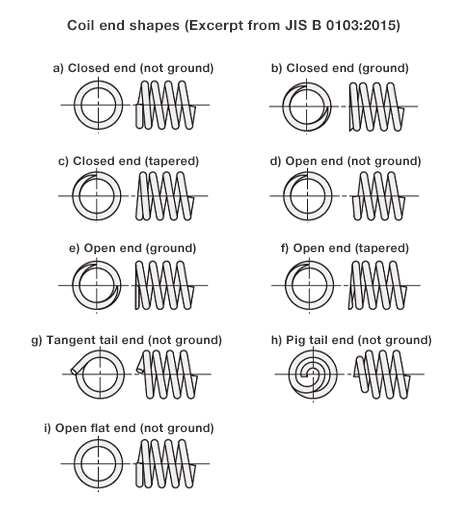
X1 and X2 is the number of end coils at each end of the coil
a) When the coil end is an end shape touching the next coil, and each end coil has one coil (equivalent to the end shapes (a)-(c))
X1=X2=1
As such, n = nt-2
b) When the coil end is an end shape not touching the next coil, and each coil has 0.75 coils (equivalent to the end shapes (e) to (f))
X1=X2=0.75
As such, n = nt-1.5

For tension springs

For tension springs, the effective number of coils depends on the following. However, the hook part is excluded.
n=nt

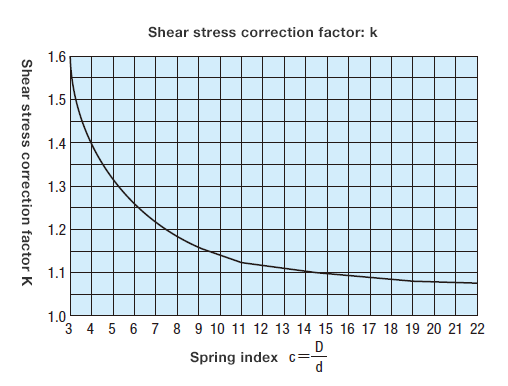
Stress correction factor

The shear stress correction factor for the spring index c value depends on the following formula or figure.

Closed length of compression spring

The closed length of compression springs can generally be calculated using the following simplified formula.
However, the closed length of compression springs must only be a reference.

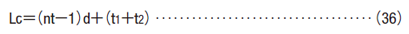
t1 + t2 is the sum of the thickness of both coil ends
If both ends of a compression spring have been ground or tapered, and especially when closed length must be specified, the value obtained from the following formula can be used as the maximum closed length. However, caution is required as, depending on the spring shape, the closed length could be larger than this value.

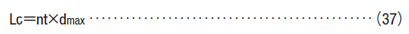
Initial tension of tension spring

Tension springs with solid coiling can cause initial tension Fi.
The initial tension can be calculated using the following formula.

When steel wire such as piano wire and hard steel wire has been formed into solid coiling but not undergone low temperature annealing, initial shear non-correction stress To,i shall be within the two diagonal lines in the figure below. However, when using wire other than steel wire and carrying out low temperature annealing, initial shear non-correction stress To,i taken from between the two diagonal lines below can be corrected as follows.

1. (1)When using stainless steel spring wire, it shall be 15% lower than the initial shear non-correction stress of steel wire.
2. (2)When carrying out low temperature annealing after the wire has been formed, it shall be 20 to 35% lower for piano wires, hard steel wires, and other steel wires, and 15 to 25% lower for stainless steel spring wires, than the values obtained above. As an alternative to obtaining the pre-low temperature annealing initial shear non-correction stress To,i from the above figure, it can also be calculated using the following empirical formula.

An example of a calculation formula used to calculate initial tension Fi through this formula is shown below.

For piano wires and hard wires [G = 7.85 × 104 (N/mm²)]

For stainless steel spring wires [G = 6.85 × 104 (N/mm²)]

Compression spring and tension spring surging

To avoid surging, the spring’s natural frequency must be selected so that it does not resonate with vibrations from the vibration source that act on the spring.
The spring’s natural frequency can be calculated using the following formula.

When both ends of compression springs and tension springs made of G = 7.85 × 10⁴ (N/mm²) material or ρ = 7.85 × 10^-6 (kg/mm³) material (such as piano wires) are either free or fixed, the spring’s first-stage natural frequency is calculated using the following formula.

Other matters for consideration

The following must also be taken into consideration for spring design equations.

(1) Spring index

As spring index gets smaller, local stress becomes excessive. Workability also becomes problematic when spring index gets either bigger or smaller. As such, when forming springs in a hot environment, spring index should be between 4 and 15, and when forming in a cold environment, spring index should be between 3 and 22.

(2) Aspect ratio

The aspect ratio (ratio of custom length to average coil diameter) of compression springs should be 0.8 or greater to maintain the effective number of coils, and 4 or below to prevent buckling.

(3) Pitch

If the pitch exceeds 0.5 D, coil diameter generally changes in line with an increase in force (load). This requires the deflection and shear stress obtained from the basic formula to be corrected, and so pitch should be kept at 0.5 D or below. General pitch estimations can be calculated using the following simplified formula.

PDF list