Tolerance Design Advantages / Calculation Examples (Tolerance Design 1)

Are you not designing only with IEB (intuition, experience, and boldness)?
Here you can get an easy-to-understand explanation of the advantages of tolerance design, and the requisite knowledge.

• What is tolerance / design?
• Tolerance design advantages / calculation examples

Tolerance design: Advantages of learning

Tolerance design has recently received renewed attention. This will explain the advantages of tolerance design.

1. 1. With tolerance calculation theory and evaluation criteria, you will be able to perform correct design.
   Even among designers who say they perform tolerance calculations, according to the survey of their actual situation, most of them respond that they were “taught by their seniors (on-the-job training)” or were “self-taught,” and many designers are “always anxious” and in fact, there are not a few designers who perform the calculations incorrectly.
   *According to the survey of approx. 15,000 designers, approx. 80% of them do not perform tolerance calculations. (Surveyed by PLANER)
   By learning tolerance design theory systematically, designers will be able to perform tolerance calculations “with confidence” and be able to properly teach it to junior staff.
   In fact, the most difficult part of tolerance design is “judgment” and “actions” for it. It is important to correctly calculate the 5 basic types of tolerance calculations such as Cp, Cpk (process capability index) and defect rate, and discuss them numerically (judgement and action).
2. 2. This can provide significant cost advantages for companies that have not traditionally performed tolerance design. （30～50%）
   Cost reductions exceeding 20% cannot be achieved by force.
   There is a limit to what can be achieved through worksite improvements and procurement efforts, and it is still impossible to achieve it unless designers “reform design.”
   There are more than 500 themes (PLANER results) where design leaders or top management realized this fact and promoted tolerance design throughout the company, resulting in cost reductions of 30% or more, and some companies have disclosed some of those.
3. 3. Design quality problems can be theoretically solved before they happen.
   There is no such thing as a design that you never know unless it is built. Everything is determined by design.
   If all parts are manufactured and assembled according to the design drawings, it is easy to calculate the probability of any defects (failures, problems) that may occur (defect rate).
   This is FMEA (Failure Modes and Effects Analysis), and it is “tolerance design” that derives the probability of defect occurrence for each of these items and improves them.
4. 4. Designers will be able to make correct evaluations of others' designs. (Check of drawing)
   If you are a design leader, you must be able to immediately evaluate and instruct your subordinates (or outsourced designers) on whether their design drawings are correct. (=check of drawing)
   As a leader, you focus on important design points and perform tolerance calculations (at the level of manual calculations). If there are any dangerous points, you call the designer to check the tolerance calculations performed by the designer, and if they are wrong, you point them out and instruct the designer to make the correct design.
   More than 90% of the drawing checker's work should be devoted to checking tolerance design.
   As a design leader, if you cannot do this, you will not be able to check drawings, and also to guide and train your subordinates.

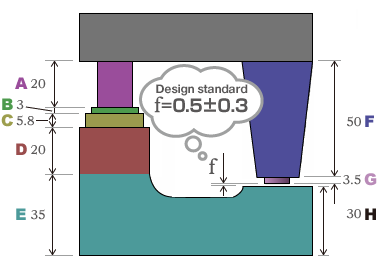
Tolerance calculation example.

The following shows some examples of tolerance calculations. Let us consider, for example, this device.
Let us study a case where gap f is a very important value and a design standard of 0.5 ±0.3 must be achieved.
This gap f is composed of all parts from A to H.
The key point is whether or not the design standard can be satisfied even if all parts from A to H vary to the limit of tolerance, and how to set the tolerance of each part is important for this reason.
Let's consider a few things here in a simple model.

Given the condition in the figure below that the χ gap must be designed in the range of 0.5 ±0.4 and the dimension of part A is 9.5 ±0.3, how would you go about calculating the dimensions and tolerances for parts B, C and D if they were the same part?

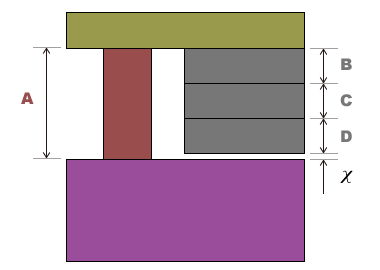
The dimensional values of B, C, and D are (9.5-0.5)/3 = 3, right? Tolerance calculations are then performed, but there are 2 major methods for calculating tolerances. Compatibility and incomplete compatibility methods.
The calculation method for the worst-case (maximum or minimum) tolerance of all parts assembled is called the compatibility method.
In contrast, the method of calculation based on statistical theory, which comes from variation and its treatment, is called the incomplete compatibility method.

In the compatibility method, the following formula is used to calculate the result, which is ±0.033.
On the other hand, the incomplete compatibility method yields a result of ±0.15.

Compatibility method
0.3+(T+T+T)=0.4
3T=0.1
T=0.033

Incomplete compatibility method
0.32+T²+T²+T²=0.4²
3T²=0.4²-0.3²
T²=0.0233
T=0.15

In other words, whether the tolerance is ±0.033 or ±0.15 depends on how the tolerance is calculated.
In this example, the difference is approx. 5-fold, and naturally, there will be a significant difference in cost.

Whichever calculation method is adopted is the company's policy and should be thoroughly confirmed; but in any case, it is important to be fully aware of this theoretical background.

PDF list